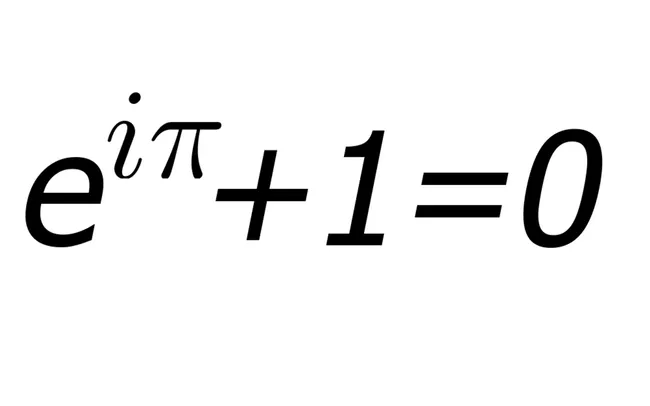
If you can't see the beauty of this equation yet then:
First, SAD! HOW? How could you not? I mean ... Okay, I'll help you.

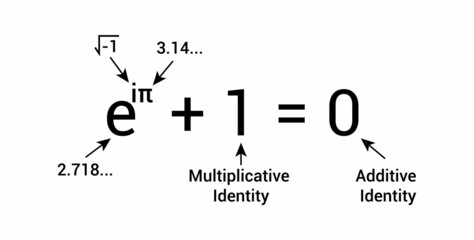
So, for the complete context, I'll explain.
The "e" here is Napier's constant, and its an irrational number, which means that it can't be expressed as a fraction.
The "i" here is called iota and its value is shown in the above image, its an imaginary number.
Everyone knows "π", our cute little irrational ratio.

So the beauty is, an imaginary number (i) when multiplied with an irrational number (π) and these raised to the power of another irrational number (e) become a whole number (i.e. '-1').

Keep in mind that "e" being an irrational number can't be expressed in the form of a rational number with any power.
So one might get quite curious that how is this equation even possible?
Well this equation comes from an another form of Euler's equation, which is also called, Euler's Identity.

It goes something like this:

The sine and cosine are trigonometric ratios that work as functions and give values corresponding to those given as input, here '∅' is the input.
And when '∅' is equal to 'π' sine takes the value 0, because sinπ = 0 and cosine takes the value -1, because cosπ = -1.
Which makes our equation:

Thankyou for bearing with me, if you think its too much, I don't blame you, but if you liked it then DUDE! I LIKE YOU!